Invariant stress and strain measures
Invariante Spannungs- und Dehnungsmaße ermöglichen es, einen allgemeinen dreidimensionalen Spannungszustand durch skalare Größen – sogenannte Invarianten – zu beschreiben. Eine Invariante ist eine Größe, die unabhängig von der Wahl des Koordinatensystems ist. Sie kann daher sowohl durch Variablen im kartesischen Grundkoordinatensystem als auch durch Variablen im Hauptachsensystem – unter Verwendung der Hauptspannungen und Hauptdehnungen – ausgedrückt werden. Es sei darauf hingewiesen, dass auch Hauptspannungen in Form von Invarianten dargestellt werden können. Neben der Möglichkeit einer einfachen grafischen Darstellung des dreidimensionalen Spannungszustands werden diese Größen auch bei der Formulierung der meisten Fließflächen verwendet.
Nachfolgend wird zur Veranschaulichung eine kurze Liste grundlegender invarianter Spannungs- und Dehnungsmaße für den Fall der triaxialen Kompression dargestellt, definiert in Abhängigkeit der Hauptspannungen und -dehnungen. Weitere Einzelheiten sind im theoretischen Handbuch zu finden.
- Mittlere Spannung
![]()
- Volumetrische Dehnung
![]()
- Äquivalente Deviatorspannung
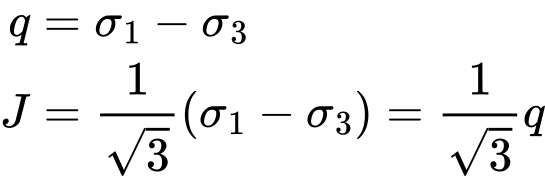
- Äquivalente Deviatorische Dehnung
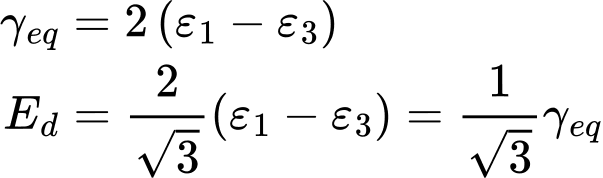
- Der Lode-Winkel wird allgemein ausgedrückt (für triaxiale Kompression gilt σ...). σ2 - σ3 = σ1 - σ3
 θ = 30°)
θ = 30°)
![]()