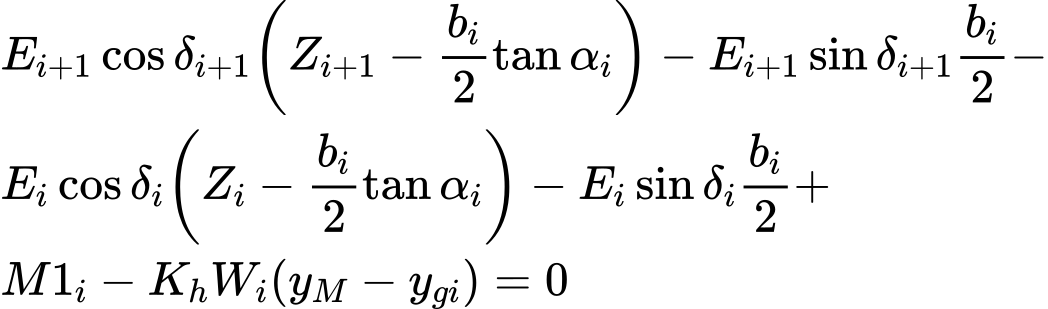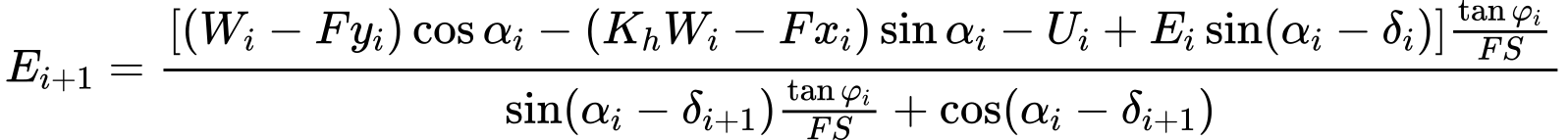Morgenstern-Price
Metoda Morgenstern-Price jest metodą paskową, opracowaną na bazie równowagi granicznej. Metoda ta wymaga spełnienia równowagi sił i momentów oddziaływujących na poszczególne bloki. Bloki tworzone są poprzez dzielenie gruntu powyżej powierzchni poślizgu, za pomocą płaszczyzn podziałowych. Siły oddziaływujące na poszczególne bloki pokazano na rysunku poniżej:
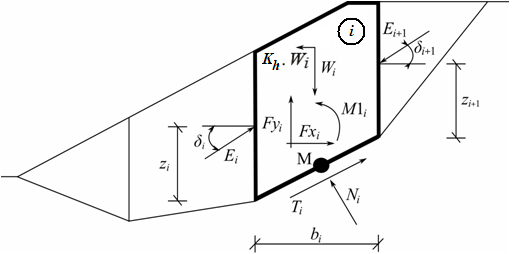 Schemat statyczny - metoda Morgenstern-Price'a
Schemat statyczny - metoda Morgenstern-Price'a
Dla każdego bloku zakłada się oddziaływanie tych samych sił, co w metodzie Spencer'a. W metodzie Morgenstern-Price'a przyjęto podane poniżej założenia, aby wyliczyć równowagę graniczną sił i momentów dla poszczególnych bloków:
- Płaszczyzny podziału między blokami są zawsze pionowe.
- Linia oddziaływania ciężaru bloku Wi przechodzi przez środek segmentu i-tego powierzchni poślizgu, reprezentowany jako punkt M.
- Normalna Ni oddziaływuje w środku segmentu i-tego powierzchni poślizgu, w punkcie M.
- Nachylenie sił Ei oddziaływujących między blokami różni się dla każdego bloku (δi), na punktach końcowych powierzchni poślizgu δ = 0.
Jedyna różnica między metodą Spencera i metodą Morgenstern-Price'a podana jest na powyższej liście założeń. Wybór kątów nachylenia δi sił Ei działających między blokami realizowany jest za pomocą funkcji "pół-sinusoidy" - wybierana jest automatycznie jedna z funkcji na poniższym rysunku. Wybór kształtu funkcji ma niewielki wpływ na wyniki ostateczne, ale odpowiedni wybór może poprawić konwergencję metody. Wartość funkcji pół-sinusoidy f(xi), na punkcie granicznym xi pomnożona przez parametr λ daje wartość kąta nachylenia δi.
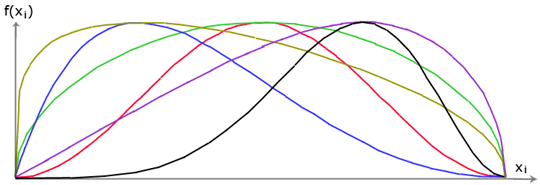 Funkcja "pół-sinusoidy"
Funkcja "pół-sinusoidy"
Rozwiązanie uwzględnia wyrażenia (1) - (5), podane w metodzie Spencera, tj.:
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
gdzie: | φi | - | kąt tarcia wewnętrznego gruntu na odcinku powierzchni poślizgu |
ci | - | spójność gruntu na odcinku powierzchni poślizgu | |
αi | - | nachylenie odcinka powierzchni poślizgu |
(1) zależność między efektywną a całkowitą wartością siły normalnej działającej na powierzchnię poślizgu.
(2) Warunek Mohra-Coulomb'a przedstawiający zależność między siłami normalnymi i tnącymi dla danego segmentu powierzchni poślizgu (Ni i Ti)
(3) równanie równowagi sił w kierunku normalnym do segmentu i-tego płaszczyzny poślizgu
(4) równanie równowagi sił wzdłuż segmentu i-tego płaszczyzny poślizgu
(5) równanie równowagi momentów wokół punktu M.
Modyfikacja równań sił (3) i (4) pozwala na uzyskanie podanego poniżej wzoru rekursywnego (6):
| (6) |
Ten wzór umożliwia wyliczenie wszystkich sił Ei, przy danych wartościach δi i SF, oddziaływujących między blokami. Rozwiązanie przyjmuje, że na początku powierzchni poślizgu, znana jest wartość E i jest równa E1=0.
Dodatkowy wzór rekursywny (7) wynika z równania równowagi momentów (5) i jest następujący:
| (7) |
Ten wzór pozwala na obliczenie, przy danych wartościach δi, wszystkich ramion sił oddziaływujących między blokami, przy znanej wartości po lewej stronie na początku płaszczyzny poślizgu, gdzie z1 = 0.
Współczynnik bezpieczeństwa SF wyznaczany jest za pomocą podanego poniżej procesu iteracyjnego:
- Wartość początkowa kątów δi ustawiona jest zgodnie z funkcją półsinusoidy (δi = λ*f(xi)).
- Współczynnik bezpieczeństwa SF dla danej wartości δi wynika z równania (6), jeśli przyjmiemy wartość En+1 = 0 na końcu powierzchni poślizgu.
- Wartość δi otrzymuje się z równania (7), z wykorzystaniem wartości Ei wyznaczonych w uprzednim kroku, przy wymaganiu zerowego momentu na ostatnim bloku. Wartości funkcyjne f(xi) są takie same przez cały czas podczas iteracji, tylko parametr λ jest iterowany. Z równania (7) nie jest wyznaczana wartość zn+1 ponieważ jest równa zeru. Dla tej wartości musi być spełnione równanie równowagi momentów (5).
- Następnie powtarzane są kroki 2 i 3, dopóki wartość δi (odpowiednio parameter λ) nie będzie się zmieniać.
Aby uzyskać stabilny proces iteracji, konieczne jest unikanie niestabilnych rozwiązań. Takie niestabilności pojawiają się w miejscach, gdy zachodzi dzielenie przez zero w równaniach (6) i (7). W równaniu (7) dzielenie przez zero występuje dla δ = π/2 lub δ = -π/2. Tak więc, wartość kąta δimusi się zawierać w przedziale (-π/2 ; π/2).
Dzielenie przez zero w wyrażeniu (6) pojawia się gdy:
![]()
Innym sprawdzeniem zapobiegającym niestabilności numerycznej jest weryfikacja parametru mα - musi być spełniony podany poniżej warunek:
![]()
Tak więc, przed wykonaniem iteracji, wymagane jest znalezienie najwyższych wartości krytycznych (SFmin) spełniających wyżej podane warunki. Wartości poniżej wartości krytycznej SFmin znajdują się w obszarze rozwiązań niestabilnych, tak więc iterację rozpoczyna się od ustawienia wartości SF na wartość "tuż" powyżej SFmin, a wszystkie wartości wynikowe SF z iteracji są wyższe niż SFmin.
Należy zwrócic uwagę na fakt, że metody rygorystyczne konwergują znacznie gorzej niż metody prostsze (Bishop, Fellenius). Problemy z konwergencją mogą wystąpić, np. w przypadku wystąpienia zbyt stromych odcinków powierzchni poślizgu, skomplikowanej geometrii, czy znaczących, gwałtownych przyrostów obciążeń. Jeśli wynik nie zostanie uzyskany zaleca się drobną korektę wprowadzonych danych, np. zdefiniowanie mniej stromej powierzchni poślizgu, zdefiniowanie większej liczby punktów definiujących powierzchnię poślizgu. Innym rozwiązaniem może być zastosowanie prostszej metody obliczeniowej.
Literatura:
Morgenstern, N.R., and Price, V.E. 1965. The analysis of the stability of general slip surfaces. Géotechnique, 15(1): 79-93.
Morgenstern, N.R., and Price, V.E. 1967. A numerical method for solving the equations of stability of general slip surfaces. Computer Journal, 9: 388-393.
Zhu, D.Y., Lee, C.F., Qian, Q.H., and Chen, G.R. 2005. A concise algorithm for computing the factor of safety using the Morgenstern-Price method. Canadian Geotechnical Journal, 42(1): 272-278.