Model Hoeka-Browna
Model materiałowy Hoeka-Browna jest najczęściej stosowanym kryterium zniszczenia do opisu nieliniowego zachowania się mas skalnych.
Podobnie do modelu Mohra-Coulomba, model Hoeka-Browna jest sformułowany w oparciu o trzy funkcje zniszczenia z rzutem na płaszczyznę dewiatorową w postaci nieregularnego sześciokąta. Jednak w przeciwieństwie do modelu Mohra-Coulomba, rzut powierzchni plastyczności fHB na płaszczyznę południkową jest opisany funkcją nieliniową. Jest oczywiste, że podobnie jak w modelu Mohra-Coulomba, kryterium plastyczności Hoeka-Browna jest funkcją średniego naprężenia efektywnego σmeff oraz kąta Lode'a θ.
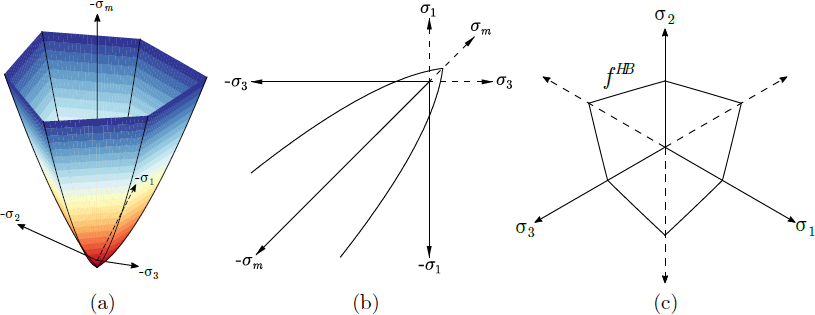a) Powierzchnia plastyczności w przestrzeni naprężeń głównych, b) rzut na płaszczyznę maksymalnego i minimalnego naprężenia głównego, c) rzut na płaszczyznę dewiatorową
Model Hoeka-Browna jest czysto empiryczny, a jego sformułowanie bazuje na wskaźniku wytrzymałości geologicznej GSI (wartość GSI = 100 odpowiada nienaruszonej skale i maleje do zera wraz z pogorszeniem jakości skały), współczynniku zaburzeń D (uwzględnia on wcześniejsze działania podziemne, w tym górnictwo i wykopy, wartość D = 0 odpowiada nienaruszonej skale, a maksymalny stopień uszkodzenia jest reprezentowany przez wartość D = 1), jednoosiowej wytrzymałości na ściskanie nienaruszonej skały σci oraz parametru mi. Dwa ostatnie parametry są wyznaczane na podstawie badania trójosiowego. Fizycznie akceptowalna maksymalna wartość zalecanej wytrzymałości na rozciąganie 
jest określana za pomocą wzoru:
gdzie parametr s i zredukowana stała Hoeka-Browna mb są wyznaczane z wykorzystaniem parametrów GSI i D, jako:
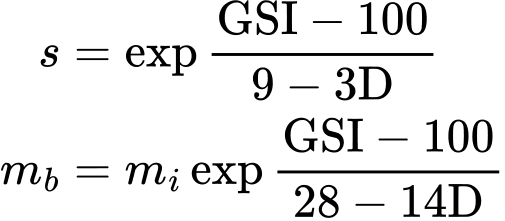
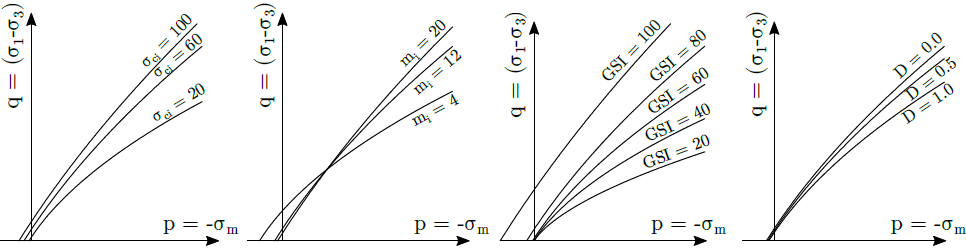
Wpływ poszczególnych parametrów na projekcję powierzchni plastyczności na powierzchnię południkową ilustruje poniższy rysunek.
Model Hoeka-Browna wymaga wprowadzenia modułu sprężystości masywu skalnego Erm, który uwzględnia stan uszkodzenia górotworu. Można go wyznaczyć np. za pomocą parametrów modelu GSI, D i σci [2]:
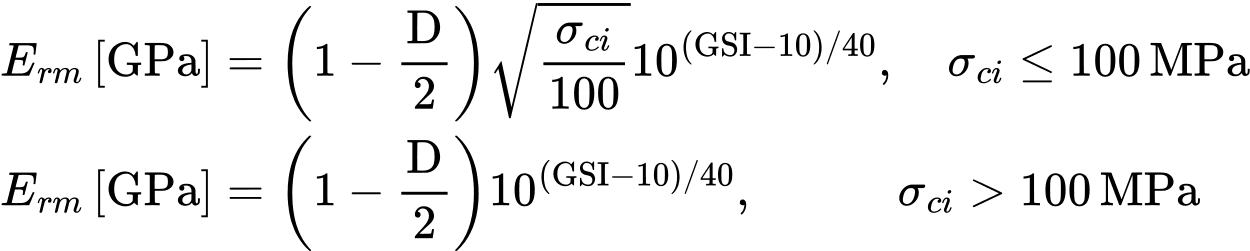
Dalsze opcje są dostępne w [3].
Parametr modelu a dostosowujący definicję zależności potęgowej w powierzchni plastyczności można również określić za pomocą wskaźnika wytrzymałości geologicznej GSI w następujący sposób:
Parametry modelu przedstawiono w poniższej tabeli.
Symbol | Jednostka | Opis | |
| [MPa] | Moduł sprężystości masywu skalnego | |
| [-] | Współczynnik Poissona | |
| [MPa] | Wytrzymałość na ściskanie jednoosiowe | |
| [-] | Stała Hoeka-Browna | |
GSI | [-] | Wskaźnik wytrzymałości geologicznej | |
D | [-] | Współczynnik naruszenia | |
| [°] | Kąt dylatancji (definiowana jest wartość początkowa | |
| [kN/m3] | Ciężar objętościowy | |
| [-] | Zredukowana stała Hoeka-Browna (definiowana lub wyznaczana z GSI, D, | |
| [-] | Stała materiałowa (definiowana lub wyznaczana z GSI, D) | |
| [kPa] | Maksymalna dopuszczalna wytrzymałość na rozciąganie | |
TsRF | [-] | Współczynnik redukcji wytrzymałości na rozciąganie (0,1), jeśli zdefiniowany, wówczas | |
| [kPa] | Graniczna wartość ciśnienia ograniczającego do modelowania dylatancji | |
| [1/K] | Współczynnik rozszerzalności cieplnej (w przypadku uwzględnienia wpływu temperatury) |
, por. rysunek)
)
Prawo płynięcia, analogicznie do modeli Druckera-Pragera i Mohra-Coulomba, jest co do zasady niestowarzyszone. Umożliwia zatem modelowanie dylatancji (rozwój dodatnich plastycznych odkształceń objętościowych podczas ścinania plastycznego) poprzez wprowadzenie kąta dylatancji ψ. Jednakże, kąt dylatancji nie jest koniecznie stały, lecz może się zmieniać, jak pokazano na poniższym rysunku.
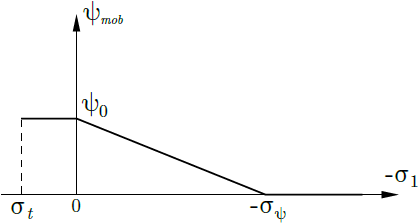
Implementacja modelu Hoeka-Browna automatycznie wprowadza wartość maksymalnej wytrzymałości na rozciąganie 
. Wartość ta może być określona lub obliczona na podstawie współczynnika redukcji wytrzymałości na rozciąganie TsRF (patrz tabela parametrów modelu). Ograniczenie wytrzymałości na rozciąganie jest napędzane, podobnie jak w modelu Mohra-Coulomba, przez powierzchnię plastyczności Rankina.
Model Hoeka-Browna umożliwia przeprowadzenie analizy stateczności. Można przeprowadzić zarówno standardową analizę stateczności zbocza jak i analizę stateczności w konkretnej fazie budowy. Jednak w przeciwieństwie do modelu Mohra-Coulomba, model Hoeka-Browna wprowadza parametr η, który zmniejsza jednoosiową wytrzymałość na ściskanie σci. Parametr ten jest wyrażony za pomocą parametru redukcyjnego ζ, który z kolei zmniejsza parametry wytrzymałości na ścinanie φ, c w modelach typu Mohra-Coulomba. Współczynnik bezpieczeństwa jest zatem równy ζ. Więcej szczegółów można znaleźć w podręczniku teoretycznym.
Często cytowana analogia do modelu Mohra-Coulomba jest szczegółowo opisana w tym miejscu. Odpowiedź modelu Hoeka-Browna w porównaniu z modelem Mohra-Coulomba jest zilustrowana w podręczniku teoretycznym poprzez symulację prostych badań laboratoryjnych.
Implementacja modelu materiałowego Hoeka-Browna w programie GEO5 MES jest szczegółowo opisana w podręczniku teoretycznym. Więcej informacji można znaleźć w poniższej literaturze.
Literatura:
[1] E. Hoek and E.T. Brown, Practical estimates of rock mass strength, International Journal of Rock Mechanics and Mining Sciences, 34.8 (1997), 1165-1186
[2] E. Hoek, C. Carranza-Torres and B. Corkum, Hoek-Brown failure criterion - 2002 edition, Proceedings of the 5th North American symposium - NARMS-TAC (2002)
[3] E. Hoek, M.S Diederichs, Empirical estimation of rock mass modulus, International Journal of Rock Mechanics \& Mining Sciences, 43 (2006), 203-215