Model Zmodyfikowany Mohra-Coulomba (MCM)
Zmodyfikowany model Mohra-Coulomba stanowi pewne rozszerzenie oryginalnego modelu Mohra-Coulomba. Powierzchnia plastyczności jest przedstawiona, podobnie jak powierzchnia plastyczności ścinania modelu Soft soil lub graniczna powierzchnia plastyczności modelu Hardening soil, w postaci kryterium zniszczenia Matsuoka-Nakai. Graficzne przedstawienie powierzchni plastyczności zostało pokazane na poniższym rysunku. Z rzutu powierzchni plastyczności na płaszczyznę dewiatorową wynika, że wraz ze zmniejszaniem się kąta tarcia wewnętrznego φ powierzchnia plastyczności zbliża się do modelu Druckera-Pragera, podczas gdy dla większych wartości φ zbliża się do powierzchni plastyczności Rankine'a. Ponadto powierzchnia plastyczności zmodyfikowanego modelu Mohra-Coulomba jest gładką krzywą wypukłą i przechodzi przez wszystkie wierzchołki modelu Mohra-Coulomba. Dlatego, w przeciwieństwie do modelu Druckera-Pragera, nachylenie rzutu na płaszczyznę południkową Mφθ nie jest stałe, lecz zależy od aktualnej wartości kąta Lode'a Mφθ = Mφθ(φ, θ).
Wręcz przeciwnie, funkcja potencjału plastycznego, która napędza ewolucję odkształceń plastycznych, jest identyczna z funkcją z modelu Druckera-Pragera. Jest wobec tego niezależna od kąta kąta Lode'a. Niemniej jednak zależy od kąta dylatancji ψ (Mψ = Mψ(ψ)). Ogólnie przyjmujemy, że φ ≠ ψ, co odpowiada niestowarzyszonemu prawu płynięcia.
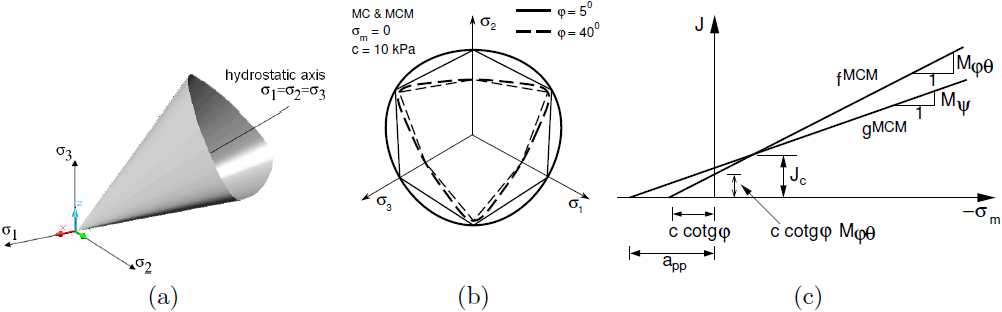a) powierzchnia plastyczności w przestrzeni naprężeń głównych, b) rzut na płaszczyzny dewiatoryczne i c) płaszczyzny południkowe
W przeciwieństwie do wszystkich pozostałych modeli, niezależnie czy sprężysto-idealnie plastycznych czy sprężysto-plastycznych ze wzmocnieniem/osłabieniem, model zmodyfikowany Mohra-Coulomba pozwala na rozwój powierzchni plastyczności jako funkcji równoważnego dewiatorowego odkształcenia plastycznego Edpl. Dokładniej rzecz ujmując, definiujemy funkcje c(Edpl) oraz φ(Edpl). Zakładana, odcinkowo liniowa, zmienność parametrów wytrzymałościowych jest widoczna na poniższym rysunku.
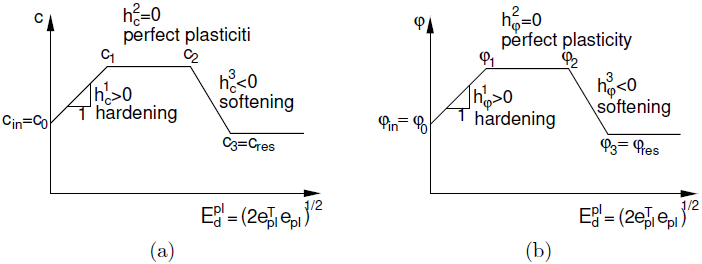Rozwój parametrów wytrzymałości na ścinanie w funkcji równoważnego dewiatorowego odkształcenia plastycznego Edpl: a) spójność c b) kąt tarcia wewnętrznego φ
Ograniczając uwagę do prostych badań laboratoryjnych (np. trójosiowego ściskania) oraz do sprężysto-idealnie plastycznej odpowiedzi model dostarcza przewidywań identycznych z tymi generowanymi przez model Druckera-Pragera lub model Mohra-Coulomba.
To samo dotyczy zastosowania warunków z lub bez odpływu. Więcej informacji na ten temat można znaleźć w prezentacji modelu Druckera-Pragera. Przeprowadzając analizę w warunkach bez odpływu, wykorzystując jednocześnie cechy wzmocnienia/osłabienia, można zastosować wyłącznie Typ (1): analiza w naprężeniach efektywnych (cef, φe).
Modelując wpływ dylatancji (ewolucji dodatnich objętościowych odkształceń plastycznych podczas ścinania plastycznego) zmodyfikowany model Mohra-Coulomba pozwala na uwzględnienie albo stałej wartości kąta dylatancji ψ, podobnie do modeli Druckera-Pragera, Mohra-Coulomba, Hoeka-Browna, lub na opisanie rozwoju ψ z wykorzystaniem teorii dylatancji Rowe’a w następujący sposób:
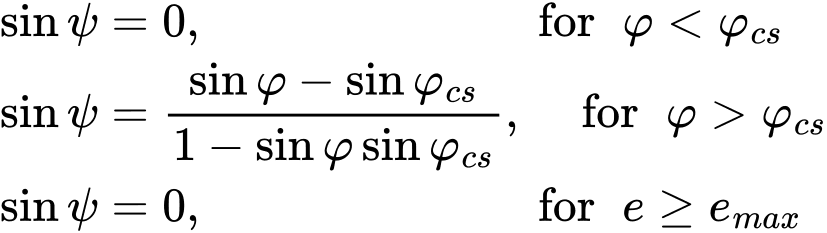
gdzie φ reprezentuje aktualną wartość kąta tarcia wewnętrznego, a φcs jest kątem tarcia stanu krytycznego. Oczywiste jest, że rozwój dodatnich odkształceń objętościowych można ograniczyć za pomocą maksymalnego wskaźnika porowatości emax jak wyjaśniono na przykład w opisie modelu Druckera-Pragera.
Parametry definiujące zmodyfikowany model Mohra-Coulomba przedstawiono w poniższej tabeli. Parametry użyte w analizie w warunkach bez odpływu typu 2 i 3, można znaleźć w prezentacji modelu Druckera-Pragera.
Symbol | Jednostka | Opis | |
| [MPa] | Moduł sprężystości | |
| [MPa] | Moduł odciążenie/dociążenie | |
|
| Współczynnik Poissona | |
| [kPa] | Spójność efektywna | |
| [°] | Efektywny kąt tarcia wewnętrznego | |
| [°] | Kąt dylatancji | |
| [kN/m3] | Ciężar objętościowy | |
|
| Początkowy wskaźnik porowatości odpowiadający stanowi z końca 1. fazy obliczeniowej | |
|
| Maksymalny wskaźnik porowatości do zakończenia dylatancji (przy ograniczeniu dylatacji) | |
| [°] | Kąt tarcia wewnętrznego stanu krytycznego (w przypadku określania | |
| [1/K] | Współczynnik rozszerzalności cieplnej (w przypadku uwzględnienia wpływu temperatury) | |
| - | wykres prezentujący rozwój c w funkcji |
za pomocą teorii dylatancji Rowe'a)
(w przypadku uwzględnienia wzmocnienia/osłabienia)Zmodyfikowany model Mohra-Coulomba umożliwia przeprowadzenie analizy stateczności. Można przeprowadzić zarówno standardową analizę stateczności zbocza jak i analizę stateczności w obrębie danej fazy budowy. Zadanie to rozwiązuje się poprzez stopniową redukcję maksymalnych wartości parametrów wytrzymałości na ścinanie c, φ w sposób analogiczny do opisanego w odniesieniu do modelu Druckera-Pragera. Podczas procesu stopniowej redukcji funkcja wzmocnienia/osłabienia jest wyłączana.
Oczekuje się, że model zostanie dodatkowo udoskonalony poprzez wprowadzenie powierzchni plastyczności cap, podobnie jak w modelu Soft soil.