Pomoc online

Modele nieliniowe

Wprowadzenie nieliniowych modeli materiałowych pozwala na znaczną poprawę w zakresie uchwycenia rzeczywistej odpowiedzi gruntów na przyłożone obciążenie. W programie GEO5 MES modele te są formułowane z wykorzystaniem teorii plastyczności lub hipoplastyczności. Zastosowanie modeli nieliniowych zazwyczaj wiąże się z rozwojem odkształceń plastycznych. Odkształcenia te można wykorzystać do graficznego wskazania potencjalnych stref zniszczenia, np. w postaci zlokalizowanego równoważnego dewiatorowego odkształcenia plastycznego. Teoria hipoplastyczności nie oferuje takiej możliwości. Graficzną reprezentację oczekiwanych obszarów zniszczenia można w tym konkretnym przypadku uzyskać poprzez wykreślenie parametru zmobilizowanej wytrzymałości na ścinanie.

Rozwój odkształceń plastycznych jest napędzany przez powierzchnię plastyczności, reprezentującą w przestrzeni naprężeń granicę między sprężystym a plastycznym zachowaniem materiału. Matematyczne sformułowanie powierzchni plastyczności reprezentuje wówczas pewien warunek zniszczenia (funkcję plastyczności). W ogólnym stanie naprężenia powierzchnia plastyczności jest zazwyczaj formułowana za pomocą niezmienniczych miar naprężenia i odkształcenia. Funkcja ta pozostaje stała w całym zakresie obciążeń (sprężysto-idealnie plastyczne modele materiałowe) lub może ewoluować w zależności od aktualnego stanu naprężenia i odkształcenia plastycznego (sprężysto-plastyczne modele materiałowe ze wzmocnieniem/osłabieniem lub modele stanu krytycznego). W stanie równowagi punkt materialny zawsze znajduje się wewnątrz powierzchni plastyczności (odpowiedź sprężysta) lub na jej granicy (odpowiedź plastyczna). Więcej szczegółów można znaleźć w podręczniku teoretycznym.

Jako przykład ilustrujący rozważamy graficzną reprezentację powierzchni plastyczności Misesa w przestrzeni naprężeń głównych. Powszechny sposób wizualizacji obejmuje projekcje powierzchni plastyczności na płaszczyznę dewiatorową i południkową, gdzie

σ_m to naprężenie średnie, J to równoważna miara dewiatorowa dewiatorowych składowych naprężenia, a θ to kąt Lode'a. Płaszczyzna dewiatorowa jest prostopadła do osi hydrostatycznej, gdzie σ₁ = σ₂ = σ₃ = σ_m.

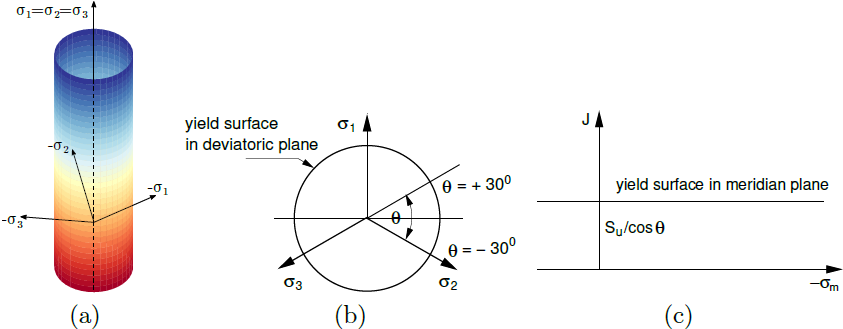a) powierzchnia plastyczności w przestrzeni naprężeń głównych, b) projekcja na płaszczyzny dewiatorowe i c) płaszczyzny południkowe

• Modele materiałowe sprężysto-idealnie plastyczne. Do tej grupy modeli materiałowych należą modele Druckera-Pragera, Mohra-Coulomba i Hoeka-Browna.
• Sprężysto-plastyczne modele materiałowe ze wzmocnieniem lub osłabieniem. Do tej grupy modeli materiałowych należą modele Hardening soil, Soft soil oraz zmodyfikowany model Mohra-Coulomba.
• Modele stanu krytycznego. Do tej grupy modeli materiałowych należą zmodyfikowany Cam-clay, uogólniony Cam-clay oraz Hypoplastic clay.

Uwaga: W przeciwieństwie do programu GEO5 MES, wyrażenia matematyczne i graficzna reprezentacja zależności konstytutywnych oraz powierzchni plastyczności i powierzchni potencjału zakładają, tak jak podano w podręczniku teoretycznym, standardową konwencję znaków teorii sprężystości, tzn. naprężenie rozciągające jest dodatnie, a naprężenie ściskające ujemne (σ > 0 - rozciąganie, σ < 0 - ściskanie).